Winston Wk 10 | First Neural Network
WINSTON - This article is part of a series.
GitHub Repository - Winston - All parts of the project are linked through submodules
Overview #
I talked last week about the plan I have to create a hand gesture recognition machine learning model. This week I started enacting the plan by creating my first neural network (following a tutorial). The neural network is simple, as it can figure out an answer based on the first column of the input data. Now, while we can pick up on that quite easily, a machine cannot as it hasn’t learnt how to do that and doesn’t have the same connections and development that a human brain has. The data would look along the lines of this:
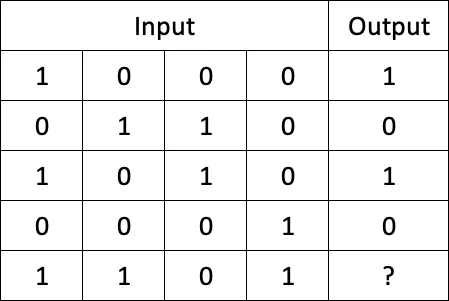
We can tell in the ?, there should be a 1, but as stated, this is what the machine will have to learn, and is what the tutorial has taught me to do.
Neural Network #
Firstly, here’s the code, and don’t worry I will break it down below:
class ArtificialNeuralNetwork:
"""
A class to represent an Artificial Neural Network.
Attributes
----------
synaptic_weights : ndarray
The weights of the synapses in the neural network.
"""
def __init__(self) -> None:
"""
Initializes the ArtificialNeuralNetwork object with random synaptic weights.
"""
self.synaptic_weights = 2 * np.random.random((4, 1)) - 1
def sigmoid(self, x) -> float:
"""
Maps a value from 0 to 1 using the sigmoid function.
Parameters
----------
x : float
The input value.
Returns
-------
float
The sigmoid of the input value.
"""
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x) -> float:
"""
Computes the derivative of the sigmoid function.
Parameters
----------
x : float
The input value.
Returns
-------
float
The derivative of the sigmoid of the input value.
"""
return x * (1-x)
def think(self, inputs) -> float:
"""
Computes the dot product of the inputs and synaptic weights, and applies the sigmoid function.
Parameters
----------
inputs : ndarray
The input values.
Returns
-------
float
The output of the neural network.
"""
inputs = inputs.astype(float)
output = self.sigmoid(np.dot(inputs, self.synaptic_weights))
return output
def train(self, training_inputs: np.ndarray, training_outputs: np.ndarray, number_of_iterations: int) -> None:
"""
Trains the neural network using the given training inputs and outputs.
It calculates the error margin by comparing the output to the expected output and adjusts the synapses based on this error margin (back propagation).
Parameters
----------
training_inputs : ndarray
The inputs that the model will train with.
training_outputs : ndarray
The expected outputs of the model.
number_of_iterations : int
The number of training iterations to run.
Returns
-------
None
"""
for _ in range(number_of_iterations):
output = self.think(training_inputs)
error = training_outputs - output
adjustments = np.dot(training_inputs.T, error *
self.sigmoid_derivative(output))
self.synaptic_weights += adjustments
if __name__ == '__main__':
ann = ArtificialNeuralNetwork()
print("Weights Pre-Training")
pprint(ann.synaptic_weights)
training_inputs = np.array([[1, 0, 0, 1],
[0, 1, 1, 0],
[1, 0, 1, 0],
[0, 0, 0, 1]])
training_outputs = np.array([[1],
[0],
[1],
[0]])
ann.train(training_inputs, training_outputs, 10000)
print('\n')
print("Weights post-Training")
pprint(ann.synaptic_weights)
_input = np.array([1, 0, 1, 0])
output = ann.think(_input)
result = decimal.Decimal(output[0]).quantize(
decimal.Decimal('1'), rounding=decimal.ROUND_HALF_UP)
print('\n')
pprint(f"The answer for {_input} is: {result}")
That’s a lot right? Lucky for all of the code commenting!
Anyway, here’s how it works.
General #
The neural network class is designed to be able to create a neural network to work with a given input, which in this case is an array with 1’s and 0’s. It is assigned random weights between 1 and -1 on creation and will then be trained over x iterations (as seen in ann.train()) and will be able to take an input and give an output based on the training it has received.
__init__ #
The __init__ function is the constructor for the class. When the class is created, it assigns the synaptic_weights attribute to a 4x1 array of random numbers between 1 and -1, simulating 4 neurons that will modify the input data to generate an output.
sigmoid #
The sigmoid function maps any value between 0 and 1 using the mathematical sigmoid function (1 / (1 + e^-x)).
sigmoid_derivative #
The sigmoid_derivative function calculates the derivative of the sigmoid function, which is used in the back propagation & training of the neural network.
think #
The think function takes an input and will multiply it by the synaptic_weights to decide on what the best answer is given the input. It uses the sigmoid function as the answer in this case is a value between 0 and 1, and will be rounded up or down afterwards.
train #
The train function is the building block of it all as it is what trains the neural network to be able to give the correct output. It runs a certain number of times that has been specified and will calculate the error margin by comparing the output to the expected output. It will then adjust the weights of the synapses through back propagation based on the error margin.
Results #
The results of the neural network are as follows (command line):
Weights Pre-Training
array([[ 0.79729058],
[-0.80537704],
[ 0.05984075],
[-0.57545079]])
Weights post-Training
array([[ 8.94996795],
[-3.50670516],
[-1.76471556],
[-4.37118727]])
'The answer for [1 0 1 0] is: 1'
'The answer for [0 1 1 0] is: 0'
This shows a large success in the training of the neural network as it has learnt to look at the first column of the input data to determine the output. This may not be a very complex ANN but it sure does get the job done and teaches me about the way that ANNs work, and means that I can start to experiment with them and test other input data out and how I can modify the code to allow it to run smoothly with what I already have. The plan is that this week I will continue to work on that and get some new form of input data working by next week, although I am unsure if I will succeed, but I will definitely give it my all as it is quite an interesting topic to learn about.
